Analyse (und Behandlung) von Raummoden
Störende Raumresonanzen sind ein bekanntes und bedeutendes Problem in der Raumakustik. Besonders in kleinen Räumen führen sie zu einem unausgeglichenen Frequenzgang mit positionsabhängigen Überhöhungen und Löchern und zu einem langen Nachklingen und Dröhnen, welches jeden Musikgenuss verdirbt und - in einem Abhörraum - eine kontrollierte Beurteilung des Bassbereichs verunmöglicht. Der Artikel zeigt, mit welchen Mitteln die modale Struktur eines Raums analysiert werden kann. Zur Sprache kommen einfache Modenrechner und komplexe FEM-Simulationen. Ausserdem wird dargelegt, wie anhand einer Messung und Darstellung des Wasserfalldiagramms die Raummoden identifiziert werden können.
(c) Dezember 2021, Markus Zehner, www.zehner.ch
Peer-Review, FEM-Simulationen: Robin Christ
Raumresonanzen sind ein physikalisches "Phänomen", das grundsätzlich in allen Räumen auftritt. Nicht selten trifft man auf die Meinung, durch nicht-parallele Wände liesse sich eine Verbesserung erzielen. Dass dem nicht so ist und die Anzahl und gesamte Energiedichte aller Moden bei gleichbleibendem Volumen im Gegenteil stets identisch bleibt, hat Professor Manfred Schröder bereits vor mehreren Jahrzehnten mathematisch bewiesen. Messungen und Simulationen bestätigen dies regelmässig. Durch nicht parallele-Wände wird aber die Voraussage darüber, bei welchen Frequenzen die Raummoden liegen, schwieriger und es braucht spezielle Berechnungsmethoden (FEM-Analyse), auf die ich in der zweiten Hälfte des Artikels eingehen werde.
Der Irrtum beruht auf der falschen Annahme, dass es nur bei parallelen Flächen zu einer kontinuierlichen Reflexion und deren Überlagerung mit sich selbst und damit zur Voraussetzung einer Modenbildung kommen kann. Im modalen Bereich eines Raums, ist allerdings der Wellencharakter der Schallausbreitung massgebend und nicht die rein geometrische Reflexion, die erst bei höheren Frequenzen zum Tragen kommt.
Der Übergang zwischen den beiden physikalischen Modellen ist durch die - nach der eben genannten Akustik-Koryphäe benannten - Schröder-Frequenz definiert. Sie hängt vom Raumvolumen und der Nachhallzeit ab und zwar in der Weise, dass sie umso höher liegt, je kleiner der Raum ist. Aus diesem Grund stellen Moden grundsätzlich ein umso grösseres Problem dar, je kleiner der Raum ist; in dem Sinne, dass dann ein grösserer Frequenzbereich vom modalen Schallverhalten betroffen ist und auch die Abstände der Moden, die modale Dichte, geringer ist.
Analyse mit Wasserfalldiagrammen
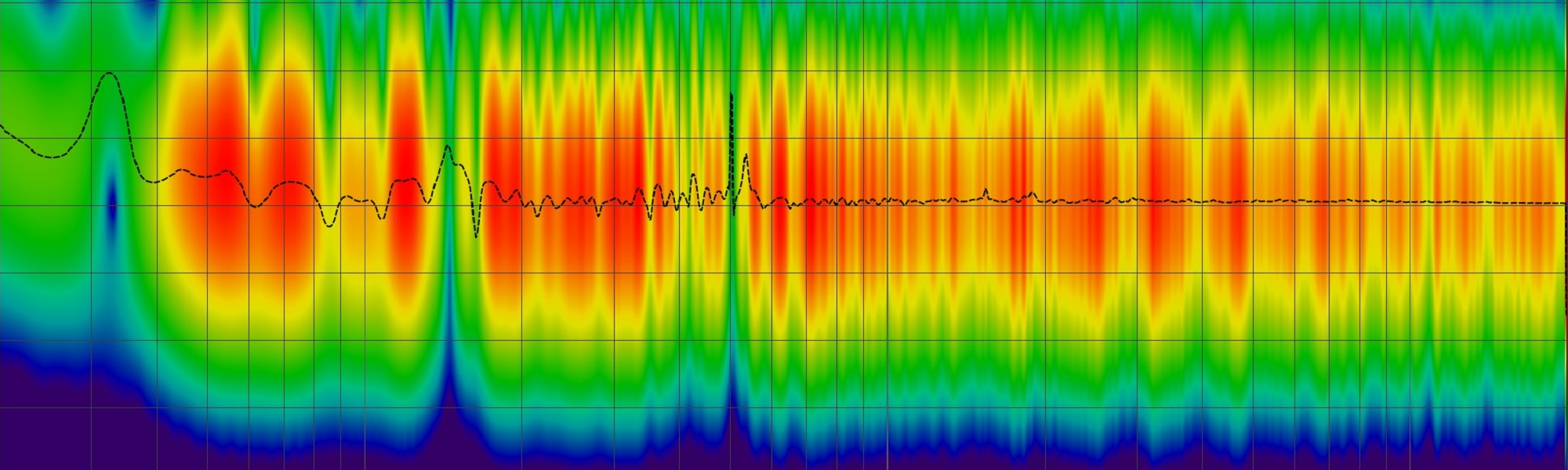
Gut sichtbar sind die Raummoden und deren Auswirkungen anhand einer Messung und der Darstellung in einem Wasserfalldiagramm. In Abbildung 1 ist dies für eine kleine, akustisch noch unbehandelte Tonstudioregie sichtbar. Deutliche Moden sind bis weit in den Mittenbereich hinein erkennbar (bis ca. 500 Hz). Die berechnete Schröderfrequenz liegt bei 430 Hz und stimmt somit gut mit dem Messergebnis überein. Oberhalb von ca. 500 Hz wird die Modendichte zunehemend so gross, dass sie in ihrer Summe ein mehr oder weniger ausgeprägtes Diffusschallfeld bilden. Unterhalb von 500 Hz passiert mit sinkender Frequenz das Gegenteil: die modale Dichte nimmt ab, es treten immer stärkere Welligkeiten und immer isoliertere Einzelfrequenzen auf. Beim Übergang der beiden physikalischen Modelle handelt es sich also nicht um eine harte Grenze sondern eher um ein Kontinuum: Zwischen den beiden Extremfällen "Modalschallfeld" und "geometrisches Schallfeld", gibt es einen über die Frequenz ausgedehnten Mischbereich.
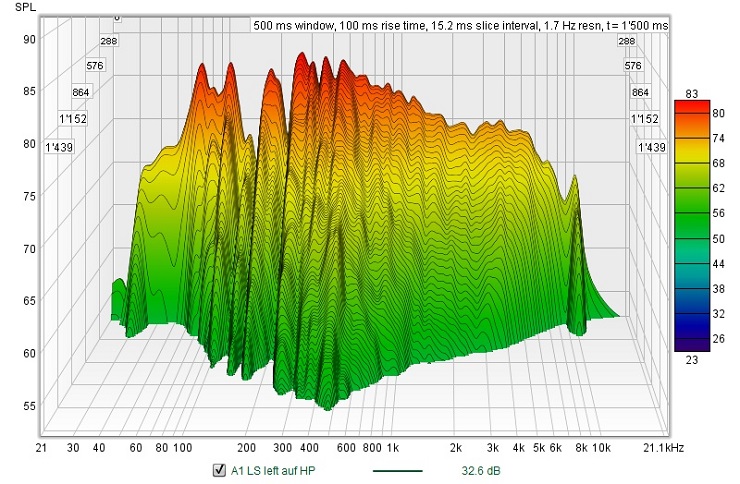
Abb. 1: Wasserfalldiagramm; in der rechten, oberen Ecke sind die wichtigsten Parameter der FFT ersichtlich
Leider ist es nicht ganz so einfach anhand der Grafik festzulegen welche der sichtbaren Raumresonanzen tatsächlich zu hörbaren Problemen führen: Man kann nicht unbedingt davon ausgehen, dass die längsten Ausläufer auch die grössten Probleme verursachen, da dies neben dem Gesamtkontext unter anderem auch wesentlich von der Frequenzlage, der Güte der Mode und deren zeitlichem Verlauf abhängt.
Weiter neigt man dazu, sich in einem Wasserfall optisch an den Ausläufern, also dem langen Nachklingen zu orientieren, während man die "Löcher" optisch tendenziell unterschätzt - letztere stechen einfach viel weniger ins (ungeübte) Auge. In der Praxis ist es aber bei einer akustischen Behandlung so, dass sich die Bekämpfung der Löcher grundsätzlich als sehr viel schwieriger darstellt, als die Überhöhungen, weshalb sie einer besonderen Beachtung bedürfen.
Es gibt im übrigen zwei Arten von Frequenzlöchern, die sich elementar unterschiedlich verhalten: Zum einen kann es sein, dass man sich genau in einem Druckknoten einer Raummode aufhält. Das Frequenzloch entsteht dann an der Messposition, während an anderen Orten im Raum bei dieser Frequenz durchaus (übermässig viel) Druck vorhanden ist. Die Lösung besteht dann darin, die Positionen von Lautsprechern und Hörer zu ändern (ich gehe später noch genauer darauf ein) oder, dass man einen Bass-Absorber einsetzt; mit diesem werden nicht nur die Dröhneffekte und die Überhöhungen im Frequenzgang reduziert, sondern auch die entstehenden Löcher in den Druckknoten.
Eine gänzlich andere Ursache kann vorliegen, wenn der Raum aufgrund seiner Geometrie eine sehr unregelmässige Verteilung der Raumresonanzen aufweist und grosse Abstände zwischen ihnen entstehen. Das Risiko, das sowas eintritt, ist umso grösser, je kleiner der Raum ist und je näher die Abmessungen der drei Raumdimensionen beieinanderliegen - oder wenn Länge, Breite und Höhe nahe an ganzzahligen Vielfachen liegen. In solchen Fällen kommt es vor, dass ein Frequenzbereich sehr viel schwächer übertragen wird, als andere, weil das Schallfeld durch keinerlei oder nur sehr wenige Moden gestützt wird. Im Gegensatz zur Auswirkung einer Raummode, wird sich diese schwächere Übertragung dann im ganzen Raum zeigen und lässt sich nicht mit Absorbern beheben. Stattdessen muss der fehlende Frequenzbereich entweder durch einen Kompensationssubwoofer erzeugt werden. Oder die den unterrepäsentierenden Frequenzbereich flankierende Moden sind so zu modifizieren, dass sie breitbandiger wirken und dadurch das Loch aufzufüllen vermögen. Theoretisch könnte man den Raum auch so modifizieren, dass zusätzliche Moden erzeugt werden, die das Loch füllen; vor allem aus platztechnischen Gründen ist dies in kleinen Räumen aber kaum praktikabel.
Eine weitere "Interpretationsfalle", die einem in die Irre führen kann, zeigt die folgende Abbildung 2: im Wasserfalldiagramm links sieht es auf den ersten Blick offensichtlich so aus, als würde der gemessene Raum um 500 kHz deutlich länger nachklingen, als um 2 kHz: Während der letzgenannte Frequenzbereich bereits nach etwa 200 ms aus der Grafik verschwunden ist, hält der ersterwähnte fast doppelt so lange an. Dieser falsche Eindruck entsteht aber nur, weil der Frequenzbereich um 500 Hz bereits einen deutlich höheren Ausgangspegel aufweist; das heisst das erste Zeitsegment, welches den Direktschall des Lautsprechers und erste frühe Reflexionen beinhaltet ist deutlich Pegelstärker. Eliminiert man diesen Effekt (in diesem Beispiel, indem man den unausgeglichenen Frequenzgang des Lautsprecher equalisiert), sieht das Bild auf einmal ganz anders aus, nämlich so wie in der Abbildung rechts. Nun sind die Abklingvorgänge annähernd gleich, der Raum verhält sich also im dargestellten Frequenzbereich ausgesprochen homogen, was sein zeitliches Verhalten betrifft.
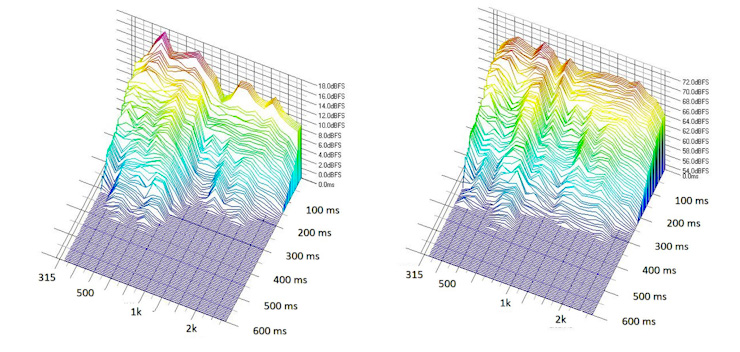Abb. 2: Pegelabhängiges Abklingverhalten im Wasserfalldiagramm
Ein Wasserfalldiagramm zeigt drei Dimensionen des Schallsignals gleichzeitig, nämlich die Frequenz (meist auf der X-Achse), den Pegel (Z-Achse/farbliche Codierung) und den zeitlichen Verlauf (Y-Achse). Um dieses Diagramm zu generieren, zerlegt die Software das Zeitsignal in einzelne Abschnitte und berechnet eine Schnelle Fourier Transformation (FFT) auf diese einzelne Zeitsegmente. Wie das Ergebnis ausfällt ist massgeblich von den Parametern abhängig, auf welcher die FFT beruht. So liegt es in der grundlegenden physikalischen Natur einer solchen Analyse, dass die Frequenzauflösung umso schlechter wird, je genauer die Zeit aufgelöst wird und umgekehrt. Man muss sich in der Praxis also entscheiden, wo man die Kompromisslinie zwischen der zeitlichen und der frequenzmässigen Verschmierung ziehen will. Dies ist anhand der folgenden Abbildungen ersichtlich.
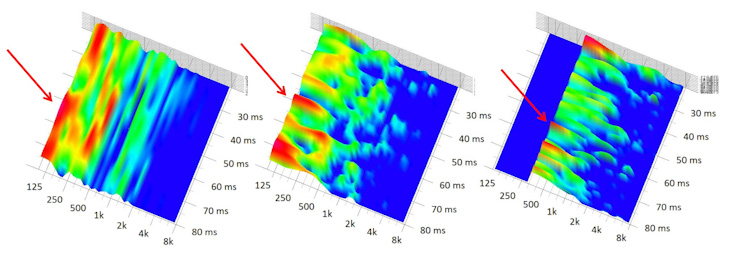Abb. 3: Wasserfalldiagramm mit unterschiedlichen FFT-Parametern
Ausgangslage ist das mittlere, hochaufgelöste Wasserfalldiagramm, welches ich erstellt habe, um für eine bestimmte Reflexion um ca. 50 Millisekunden (Pfeil) herauszufinden, welche Frequenzen sie enthält. Die zeitliche Auflösung der FFT liegt bei rund 12 Millisekunden, was es mir erlaubt, die Reflexion des Interesses zeitlich genügend gut von anderen zu isolieren. Der Nachteil ist allerdings, dass dadurch die Frequenzdarstellung derart verschmiert ist, dass die Auflösung nur noch 86 Hz beträgt (z.B. erkennbar an den durchgehend, breiten "Bergkämmen" zwischen 125 und 250 Hz).
Versuche ich nun, eine bessere Frequenzauflösung zu erreichen, sagen wir z.B. 22 Hz (also rund Faktor 4 besser), dann hat dies zur Folge, dass sich die zeitliche Auflösung um ungefähr Faktor 4 verschlechtert, nämlich auf ca. 46 Millisekunden. Dies ist im linken Wasserfalldiagramm dargestellt. Die bessere Frequenzauflösung geht nun mit einer zeitlichen Verschmierung einher, die es nicht mehr erlaubt, die gewünschte Reflexion zeitlich isoliert von anderen zu betrachten.
Beim Wasserfalldiagramm ganz rechts habe ich schliesslich die Zeit noch stärker segmentiert als im Ausgangsbeispiel, nämlich auf 2,9 ms, wodurch eine noch genauere Analyse im Zeitbereich auftritt (wann genau trifft die Reflexion ein und wie lange dauert sie an?). Dadurch sinkt nun allerdings die Frequenzauflösung auf rund 345 Hz (u.a. daran zu erkennen, dass unterhalb von dieser Grenzfrequenz gar nichts mehr dargestellt wird). Man beachte anahnd der drei Beispiele auch, wie sich der angezeigte Pegel (hier durch die Farben ersichtlich) abhängig von den Einstellungen verändert.
Wie das Ergebnis einer Wasserfallanalyse optisch dargestellt wird, und damit auch welche Informationen daraus zu gewinnen sind und welche Details unsichtbar bleiben, ist also sehr stark von den eingestellten FFT-Parametern abhängig. Neben den erwähnten Punkten spielen auch der Fenstertyp ("Windowing"), Definition und Verlauf einer allfälligen Überlappung der einzelnen Analyseabschnitte und weitere Einstellparameter eine Rolle. Bei sehr einfachen Messprogrammen sind (die meisten) dieser Einstellungen manchmal fix vorgegeben - nicht selten ohne, dass der Anwender sich den daraus folgenden Konsequenzen für die Interpretation überhaupt bewusst ist. Bei professionellen Mess-Programm kann man die genannten Einstellungen als Anwender selber vornehmen - und damit aus ein- und denselben Daten nahezu jede beliebige Grafik "basteln".
Oder anders gesagt: traue keinem Wasserfalldiagramm, welches Du nicht selber angefertigt hast. Am ehesten eigen sich die Grafiken für direkte, unter identischen Einstellbedingungen generierte Vorher-/Nachher-Vergleiche, etwa wenn akustische Elemente in den Raum eingebracht oder aus diesem entfernt werden. Ein einzelnes Diagramm ohne Kenntnis der dahinterstehenden Berechnung ist hingegen fast vollständig nutzlos!
Behandlungsmöglichkeiten
Um die negativen Effekte der Raummoden zu beseitigen oder wenigstens zu reduzieren, kommen verschiedene Prinzipien von Bassabsorbern in Frage. Verbundplattenresonatoren bieten prinzipbedingt die grösste Breitbandigkeit, während Membran-, Platten- und Helmholtzresonatoren auf sehr viel kleinere Frequenzbereiche wirken und deshalb bevorzugt zur Reduktion von einzelnen, stark dominierenden Raummoden eingesetzt werden. Auch poröse Absorber können eingesetzt und breitbandig ausgelegt werden, allerdings benötigen sie verhältnismässig viel Platz.
Platz ist ohnehin ein Thema: Der Bassbereich erfordert oft grosse Flächen und Volumina, um beruhigt zu werden. Wenn man sich nun noch einmal in Erinnerung ruft, dass modale Probleme mit sinkender Raumgrösse zunehmen und proportional ohnehin schon weniger Platz für Massnahmen zur Verfügung steht, wird rasch klar, dass es oft darum geht, die maximale Effizienz bei möglichst geringem Platzbedarf zu erreichen. Deshalb ist es nicht nur wichtig die passende Massnahme zu definieren, sondern auch sicherzustellen, dass das Akustikelement am bestmöglichen Platz steht.
Bei sehr geringem Platzbedarf oder wenn keine Akustikbauten möglich sind, kann unter Umständen auch eine elektronische Bassfalle (aktiver Absorber) eine Alternative zu passiven Massnahmen darstellen. Ich habe dieses Wirkprinzip bereits vor längerer Zeit in einem ausführlichen Artikel vorgestellt.
Klassische, geometrische Modenberechnung
Wie sich die Raummoden äussern, das heisst an welchen Positionen sich bei welchen Frequenzen Überhöhungen und Senken ergeben, ist seit vielen Jahrzehnten hinreichend bekannt - mindestens, wenn es sich um einfache, quaderförmige Räume handelt. Im Internet gibt es Dutzende von kostenlosen Seiten, auf denen man solche Berechnungen einfach und schnell durchführen kann - ansonsten tun es auch ein Taschenrechner oder eine Tabellenkalkulation, andere geben sich mit dem eigenen Kopf zufrieden.
Einer der besten Online-Kalkulatoren, ist meiner Meinung nach der "AMROC Room Mode Calculator" von Andy Melcher. Nach der Eingabe der Raumdimensionen in diesen (Länge, Breite, Höhe), werden übersichtlich alle auftretenden Moden im Raum auf einer Frequenzachse dargestellt (Abb 4, oben) und zwar sowohl die axialen (zwischen einem Wandpaar auftretend; lange rote Striche), die tangentialen (zwei beteiligte Wandpaare; kürzere violette Striche) und die obliquen (drei Wandpaare; noch kürzere, violette Striche). Wird eine der Raummoden angewählt, wird die entsprechende Sinusfrequenz gleich über Lautsprecher abgespielt und neben weiteren Angaben, ist in einer Druckdarstellung ersichtlich, wo im Raum sich eine Überhöhung ergibt (blaue/rote Farbe) und an welchen Stellen der Druck niedrig ist, also tendenziell ein Loch entsteht.
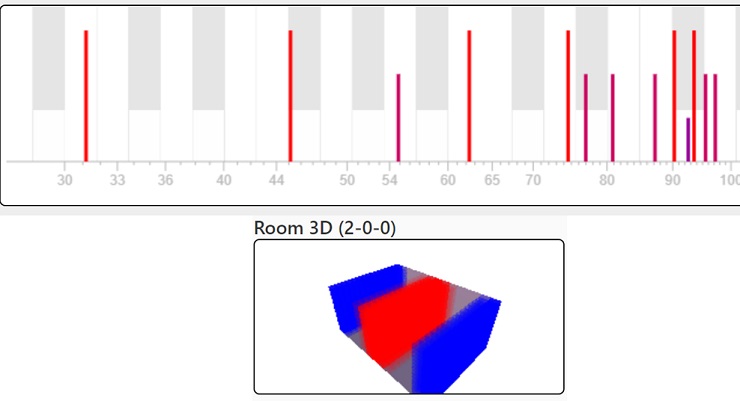
Abb. 4 Darstellung der Raumoden (oben) und Druckbild (unten) eines einfachen Modenrechners
Obige Abbildung 4 aus dem AMROC-Kalkulator zeigt in der unteren Hälfte die räumliche Druckverteilung bei der zweiten Längsmode eines Raums (2-0-0). Daraus kann man nun erkennen, dass an den Wänden hinten und vorne (blau) und genau in der Mitte des Raums (rot) der maximale Druck vorliegt. Platziert man einen Hörer an diese Stelle(n), wird die dazugehörende Frequenz also besonders laut wiedergegeben. An den Positionen dazwischen hingegen, entsteht ein Frequenzloch.
Wollte man nun diese Raummode bedämpfen, indem man einen Resonator einsetzt der auf Schalldruck reagiert, müsste man diesen also an der Frontwand oder der Rückwand oder (eher unrealistisch) in der Mitte des Raums platzieren, um den maximalen Effekt, die höchste Effizienz zu erreichen.
Die oben gezeigten Überlegungen können also sehr hilfreich sein, um akustische Konzepte zu entwickeln und sinnvolle Absorberpositionen aber auch die Platzierung von Lautsprechern und Hörposition festzulegen. Bei einem Neubau kann ausserdem geprüft werden, welche Dimensionsverhältnisse zu einer möglichst gleichmässigen Modenverteilung über die Frequenz führen. Allerdings muss man sich auch den Einschränkungen von solchen, naturgemäss sehr einfachen Berechnungen bewusst sein:
- die Kalkulationen sind nur für quaderförmige Räume anwendbar.
- die Ergebnisse sind nur dann genau, wenn die Begrenzungsflächen des Raums eine sehr hohe Oberflächenimpedanz aufweisen (z.B. dickes Mauerwerk, Betonschale etc.) und homogen zusammengesetzt sind (keine Fenster! keine Türen!)
- (grössere) Möbel und Einrichtungsgegenstände beeinflussen die Raummoden, indem sie diese frequenzmässig verschieben oder verziehen und somit die räumlichen Druck-Muster beeinflussen. Durch Einrichtungsgegenstände können auch neue, zusätzliche Moden erzeugt werden oder andere, die der Kalkulator ausgibt, können in der Praxis verschwinden.
- einzelne Moden können zwar sehr gut betrachtet werden. Allerdings ist es ausgesprochen schwierig abzusehen, wie sich die Überlagerung aller Moden mit deren komplexen Phasenbeziehungen an einem bestimmten Hörort tatsächlich auswirken.
Je mehr vom idealen, leeren, quaderförmigen, schallharten Raum abgewichen wird, desto grösser wird also zwangsläufig die Differenz zwischen Simulation und Realität.
Derartige Modenrechner stellen ausserdem lediglich die theoretische Lage der einzelnen Moden dar. Wie stark eine bestimmte Raumresonanz aber tatsächlich angeregt wird, ist davon abhängig, wie die Schallquelle in diese spezifische Mode einkoppelt, also an welcher Stelle die Lautsprecher stehen. Ob und wie eine Mode hörbar wird, ist wiederum davon abhängig, wie stark an der Stelle des Hörers an die Mode angekoppelt wird. Quellen und Hörposition und deren komplexes modales Zusammenspiel bleiben folglich von solchen einfachen Simulationen unberücksichtigt.
Zusammenfassend kann man sagen, dass die beschriebenen Modenrechner natürliche Einschränkungen aufweisen, die im besten Fall durch Erfahrung und Logik aufgewogen werden. Grundsätzlich können sie aber auch dem interessierten Laien mit etwas Akustik-Hintergrundwissen wertvolle Dienste erweisen und sie sind sehr einfach zu bedienen.
Spiegelquellen-Simulationen
Grundsätzlich den gleichen Einschränkungen unterworfen sind Modensimulationen, welche Spiegelschallquellen-Techniken anwenden (statt wie oben nur die rein geometrischen Abmessungen zu berücksichtigen). In einigen Fällen können sie aber auch Resultate für etwas kompliziertere Raumformen (z.B. Asymmetrien, L-Form etc.) liefern. Prinzipbedingt können aber mit Spiegelquellen oft nicht alle Moden identifiziert werden und unter Umständen kann es auch zu falschen Spiegelquellen kommen, die dann Moden suggerieren, die es in Wirklichkeit gar nicht gibt. Dafür werden die Positionen der Quellen (Einkopplung) korrekt berücksichtigt und der resultierende Amplitudenfrequenzgang an der gewählten Empfangsposition kann dargestell werden.
Ein Beispiel einer auf Spiegelquellen basierende Simulation ist der in der Mess-Software REW enthaltene "Room Simulator".
FEM-Simulationen
Sind genauere Prognosen nötig, als sie mit einfachen Modenrechnern und Spiegelquellen-Simulationen möglich sind, ist leider ein sehr weiter Weg zu gehen, der für Laien nicht mehr machbar ist, sondern in die professionelle Domäne gehört. Zur Anwendung kommen dann mathematische Modellierungs- und Diskretisierungsverfahren, im Speziellen die "Finite Element Methode (FEM)". Deren Nutzung setzt vertiefte Programmierkenntnisse und ein fundiertes (vorzugsweise akademisches) Verständnis von physikalischen Prozessen und deren mathematischer Modellierung voraus. Umgesetzt werden die Berechnungen mit Mathematik-Umgebungen, welche numerische Differential-Gleichungen lösen und die Resultate grafisch darstellen können. Als Beispiele seien hier "MATLAB" oder "COMSOL Multiphysics" genannt.
In einem FEM-Modell ist zunächst die Geometrie des Raums zu modellieren (CAD-Modell), evtl. ergänzt durch akustisch relevante Einrichtungsgegenstände. Grundsätzlich kann die Geometrie dabei beliebig komplex sein. Im Hinblick auf die Beschleunigung der Rechenzeit wird man hingegen bestrebt sein, sie soweit als möglich zu vereinfachen, ohne die Qualität der Ergebnisse zu tangieren. Anschliessend werden die Flächen bzw. das Volumen des Modells diskretisiert, d.h. mit einem Netz aus einzelnen Polygonen überzogen ("Vernetzung", "Mesh"). Auf diesen einzelnen Polygonen (den finiten Elementen) werden dann die analytischen Wellengleichungen (Helmholtzgleichungen) berechnet und am Schluss wieder zu einem Gesamtergebnis zusammengesetzt.
Abb. 5: FEM-Darstellung einer 1-0-0-Mode eines Raums mit deutlich erkennbarer, auf Tetraedern basierender Mesh-Struktur (Quelle: AFMG)
Die Granularität (also die Grösse und damit Anzahl der einzelnen Polygone) definiert sich anhand der gewünschten oberen Grenzfrequenz: je höher diese ist, desto kleiner müssen die Einzelelemente sein. Die Gesamtmenge der Polygone ist ausserdem durch den vorhandenen Arbeitsspeicher (RAM) begrenzt. Logischerweise wird ausserdem der Rechenaufwand grösser, je engmaschiger das Polygon-Gitter definiert wird. Im Normalfall und abhängig vom Solver (Löser der Gleichungssysteme) steigt der Aufwand mit der Anzahl der Polygone quadratisch an (vierfacher Aufwand bei Verdoppelung der Polygone), während er bei einer Verdoppelung der Frequenz typischerweise um Faktor 8 zunimmt. Zusammengenommen (weil eine höhere Frequenz ja zwangsläufig eine feinere Gitterstruktur benötigt) hat eine Verdoppelung der Frequenz deshalb einen rund 16- bis 32-fach grösseren Rechenaufwand (pro Frequenz!) zur Folge. Um tiefere Frequenzen nicht mit unnötig vielen Polygonen zu rechnen, ist es dann unter Umständen sinnvoll, mehrere Modelle für unterschiedliche Frequenzbereiche zu verwenden und die Ergebnisse im Post-Prozessing zusammenzusetzen.
Da FEM-Berechnungen nur für den modalen Bereich des Schallfelds sinnvoll sind, muss die Granularität - und damit die Rechenzeit - umso höher ausfallen, je kleiner der Raum ist. Als Startpunkt für die obere Grenzfrequenz des Modells kann man beispielsweise das zwei- oder dreifache der berechneten Schröder-Frequenz eines Raums verwenden. Für die Simulation noch höherer Frequenzen, gelten dann andere physikalische Gesetzmässigkeiten, welche auch andere Simulations-Verfahren wie (hybrides) Raytracing erfordern. Mittels einem Frequenzcrossover können die Raytracing-Ergebnisse dann in die FEM-Resultate überblendet werden, um das Schallfeld über den gesamten Frequenzbereich hinweg korrekt darzustellen.
Randbedingungen (komplexe Impedanz)
FEM-Simulationen führen grundsätzlich zu sehr exakten Ergebnissen - weitaus präziser als die meisten Simulationen, die sonst aus der Akustik bekannt sind. Die Voraussetzung dafür ist aber selbstredend, dass die Eingabeparameter möglichst genau bekannt sind (wenn man die Geometrie des Raums falsch eingibt, werden kaum die richtigen Ergebnisse herauskommen). Eine der grössten Schwierigkeiten bei einer akustischen FEM-Simulationen stellt die Eingabe der komplexen Impedanz der einzelnen Polygone dar: Eine homogene Wand beispielsweise, deren Oberflächenimpedanz nicht unendlich hoch ist, hat zur Folge, dass bei Auftreffen der Schallwelle neben der Änderung der Amplitude auch eine frequenzabhängige Phasenverschiebung stattfindet. Aus Sicht der Schallwelle sieht es dann so aus, dass eine bestimmte Dimension (z.B. Raumlänge) nicht der geometrischen Abmessung entspricht, sondern bei jeder Frequenz eine leicht andere Länge anzusetzen ist.
Folglich müssen also die frequenzabhängigen, komplexen Impedanz-Verhältnisse aller Flächen möglichst genau bekannt sein, damit die Wellengleichungen die Deformation der Struktur durch die einfallende Schallwelle korrekt berücksichtigen können. Abgesehen von sehr einfachen und sehr schallharten Strukturen, ist es aber schwierig, diese Daten überhaupt zu eruieren. Besonders auch bei mehrschichtigen Aufbauten wie z.B. einer Leichtbau-Vorsatzschale vor einer massiven Betonschale oder auch einem Absorberaufbau auf einer Wand, stellt dies regelmässig eine Herausforderung dar.
Eine Möglichkeit, um an die Daten zu kommen, besteht darin, die einzelnen Schichten in einem Computermodell nachzubilden und daraus dann mit Hilfe einer akustischen "Transfer-Matrix-Methode (TMM)" die Impedanz zu berechnen. Wie jedes physikalische Modell, geht aber auch dieses von bestimmten Randbedingungen aus, die jeweils nur mehr oder weniger gut mit der Realität übereinstimmen. Die Erfahrung zeigt deshalb, dass die Daten der Simulation oft manuell und zum Teil recht drastisch anhand von Mess- oder Erfahrungswerten angepasst werden müssen.
Handelt es sich um einen bestehenden Raum, kann man die Oberflächenimpedanz im Prinzip auch in situ messen, beispielsweise mit einer Intensitätssonde. Die dafür nötige Ausrüstung (und damit auch die damit verbundene Dienstleistung) ist aber sehr kostspielig. Ausserdem wird die Methode umso fehlerbehafteter je tiefer die Frequenz ist (unser Thema!) und je kleiner die zu untersuchende Fläche ausfällt.
Für kleinere Flächen und Objekte kommt auch eine Messung im Impedanzrohr ("Kundtsches Rohr") in Frage. Weitere Messmöglichkeiten, etwa mittels einem Array aus Beschleunigungssensoren oder eines Laser Scanning Vibrometers können zwar hilfreich sein; allerdings hat jedes Verfahren wieder seine eigenen Vor- und Nachteile und die Methoden sind sehr aufwändig, so dass sie in der Praxis nur in seltenen Spezialfällen ausserhalb einer Laborumgebung zur Anwendung kommen.
Nebst einigen weiteren nicht immer vollständig zutreffenden Voraussetzung, wie der Annahme der Winkelunabhängigkeit der Impedanzen oder der Annahme, dass die Polygone stets lokal reagieren, stellt die grundlegende Problematik unbekannter oder nur ungefähr bekannter Impedanzen die grösste Schwachstelle und Fehlerquelle von FEM-Berechnungen dar, welche die Genauigkeit der Endergebnisse begrenzen. Nichtsdestotrotz sind die Resultate bei sorgefältiger und gewissenhafter Modellierung genügend nahe an der Realität.
Darstellung der Resultate
Sind die FEM-Berechnungen abgeschlossen, können die Ergebnisse in mannigfaltiger Form dargestellt werden, was ich nun an einigen für die Praxis relevanten Beispielen zeigen möchte.
Zunächst lassen sich die Eigenmoden des Raums darstellen, also das grundlegende, durch die Geometrie bestimmte modale Verhalten das Raums. Anschaulich erfolgt dies üblicherweise in der Form von Druckbildern. Diese Mappings können auf echte Flächen (z.B. Raumbegrenzungen) aber auch beliebige "virtuelle" Flächen (z.B. Hörerebene) oder das gesamte Volumen erfolgen: auf der Basis der Wellengleichungen lassen sich Druck und Schnelleverhältnisse prinzipiell für jeden beliebigen Punkt des Volumens darstellen.
Abbildung 6 zeigt das Modell eines leeren Raums, der für den Bau eines Tonstudios vorgesehen ist. Die Grundfläche beträgt rund 80 Quadratmeter, das Volumen ca. 350 Kubikmeter. Die Dachkonstruktion ist schräg und von einigen quer verlaufenden Stahlträgern unterbrochen und entzieht sich deshalb schon mal grundsätzlich einer modalen Analyse mittels den eingangs erwähnten, einfachen Online-Tools. Ausserdem sind (noch) einige sehr starke akustische Asymmetrien vorhanden, etwa durch eine massive Längswand vorne rechts im Bild, der eine grosse Glasfront gegenübersteht; zwei Flächen also, mit sehr unterschiedlichen Impedanzen, welche das Schallfeld ganz unterschiedlich beeinflussen. Dargestellt ist der akustische Druck in Pascal innerhalb des Raums für eine Raummode bei 55 Hz. Man kann erkennen, dass an der geplanten Hörposition des späteren Studios (ca. 5 Meter von der Frontwand - links im Bild - entfernt) nur sehr wenig Druck vorhanden ist. Im Amplitudenfrequenzgang entsteht dadurch ein tiefes Loch.
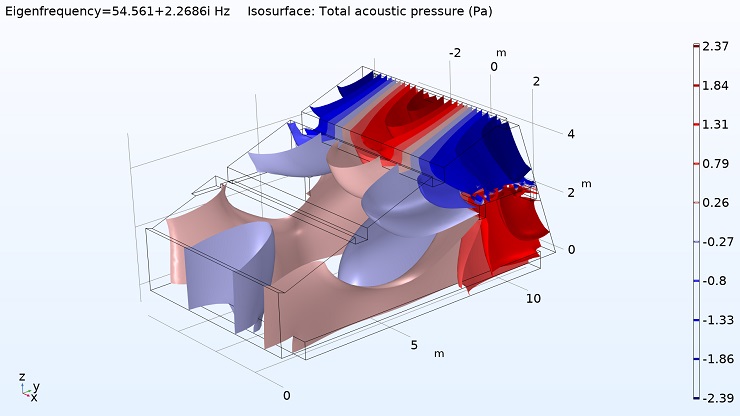
Abb. 6: FEM-Simulation - Druckverteilung innerhalb des Volumens
Abbildung 7 zeigt nun das Mapping derselben Mode, diesmal an den Raumbegrenzungsflächen, dort also, wo man in der Praxis einen Absorber platzieren kann. Will man diese Mode mit einem Resonanzabsorber bedämpfen und damit das Frequenzloch an der Abhörposition zum Verschwinden bringen, so zeigt die Grafik, dass es völlig ineffizient wäre, dies an der kleinen Frontwand zu tun, da dort (bei dieser einen Frequenz) nur sehr wenig Schalldruck vorhanden ist. Sehr viel effektivere Positionen befinden sich - offensichtlich ausschliesslich - im hinteren Teil des Raums, im Dach oder an den Seitenwänden (die Rückwand ist in dieser Grafik nicht zu sehen). Anhand der Darstellung ist auch erkennbar, dass die Mode leicht "verzogen" ist; gut zu sehen an der Decke im vorderen, niedrigen Raumbereich z.B. anhand der beiden weissen Ausöschungsschneisen, die nicht ganz parallel zueinander verlaufen. Dies ist eine direkte Folge der erwähnten Impedanzunterschiede der beiden Längswände.
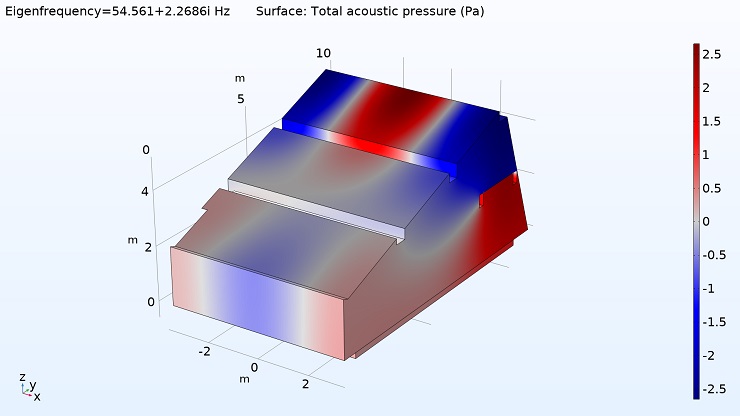
Abb. 7: FEM-Simulation - Druckverteilung an den Raumbegrenzungsflächen
Eine weitere Darstellungs-Möglichkeit eignet sich vor allem zur tiefergehenden Anlyse von Problemfrequenzen, deren Schallverhalten sich aus den statischen Druck-Bildern nicht immer ohne weiteres einwandfrei herauslesen lässt. Nötigenfalls kann eine zeitlich diskretisierte Abfolge der modalen Schallausbreitung dargestellt werden, wie im folgenden Video gezeigt.
Handelte es sich bei unserem Beispielraum um einen kleinen Konzertsaal oder um den Aufnahmeraum eines Tonstudios und würden wir noch weitere Frequenzen analysieren, könnte anhand der modalen Struktur des Raums nun ein Akustikkonzept entworfen werden; denn hierbei wäre das modale Schallverhalten im gesamten Raum zu berücksichtigen, da sich in der Praxis unterschiedlichste Instrumente an verschiedenen Raumpositionen befinden können und sich auch die Zuhörer oder die Mikrofone über einen grossen räumlichen Bereich verteilen werden.
Da es sich aber um eine Tonstudio-Regie handelt, werden sowohl die Schallquellen als auch die Hörposition nach Abschluss der Planung nicht irgendwo im Raum sein, sondern an exakt definierten Positionen. Wie oben schon angetönt, ist es nun wesentlich, in welchem Ausmass überhaupt Energie in diese Mode eingekoppelt wird.
Es empfiehlt sich deshalb, in einem nächsten Schritt, die Schallquelle zu modellieren und an der gewünschten Stelle im Modell zu platzieren. Bei kleineren Lautsprechern und tiefen Frequenzen kann dabei oft von einer simplen Kugelwellen-Ausbreitung ausgegangen werden. Ist diese Voraussetzung nicht gegeben, muss man die frequenzabhängige Richtcharakteristik des Lautsprechers (zunächst einmal kennen und dann) ebenfalls modellieren. In sehr speziellen Fällen, beispielsweise bei Quellen mit grosser Ausdehnung, kann man diese auch mit Polygonen nachbilden und an deren Knotenpunkten die Schallschnellefunktion definieren.
Ist die Quelle definiert und platziert und ist auch die Hörposition bekannt, kann nun auch die komplexe Übertragungsfunktion an letzterer dargestellt werden, also der Amplituden- und Phasenfrequenzgang. Aus dieser wiederum lässt sich über eine inverse Fourier-Transformation die Impulsantwort erzeugen und - da diese das akustische System vollständig beschreibt - auch jeder andere, beliebige akustische Parameter berechnen. Abbildung 8 zeigt als Beispiel einen Amplituden- und Phasenfrequenzgang an der Hörposition eines kleinen Abhörraums in einem Kellergeschoss.
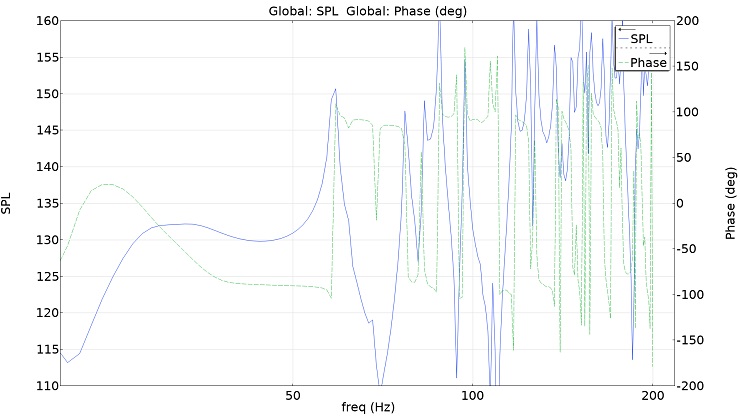
Abb. 8: Amplituden- und Phasenfrequenzgang eines unbehandelten, kleinen Studios
Nach Belieben können nun auch neue Berechnungen mit anderen möglichen Lautsprecher- und Hörpositionen erfolgen, um zu sehen, ob es bessere Aufstellungsvarianten gibt. Denkbar ist auch eine iterative Zielsuche, anhand von vorgegebenen Randbedingungen (mögliche Lautsprecher- und Hörpositionen, Definition der Zielkriterien wie z.B. ein möglichst ausgeglichener Frequenzgang). Der Algorithmus rechnet dann alle Varianten durch und spukt diejenige aus, welche den Zielkriterien am nächsten kommt.
Da es sich bei obiger Übertragungsfunktion um einen vollständig leeren Raum mit schallharten Flächen handelt, fällt das Ergebnis erwartungsgemäss ziemlich chaotisch aus. In einem nächsten Schritt können nun akustische Massnahmen definiert werden. Im einfachsten Fall werden dazu einfach die Impedanzen der betroffenen Polygone ersetzt. Es ist aber auch möglich, die tatsächlichen Materialeigenschaften der einzelnen Schichten und Bauteile eines Absorbers/Resonators zu integrieren und die Impedanzen dann anhand der physikalischen Wirkungsweise analytisch in das Modell einzurechnen. Die letztgenannte Methode ist genauer aber deutlich rechenaufwändiger.
In Abbildung 9 ist die Übertragungsfunktion nach der Definition einer ersten Stufe akustischer Massnahmen dargestellt. Das Ergebnis ist zwar noch lange nicht gut, aber schon sehr viel besser, als im ubehandelten Raum aus Abbildung 8. Iterativ kann man sich nun also an das bestmögliche Ergebnis annähern und nach Belieben diverse akustische Massnahmen virtuell ausprobieren, bis man am Schluss ein tragfähiges Akustikkonzept entwickelt hat.
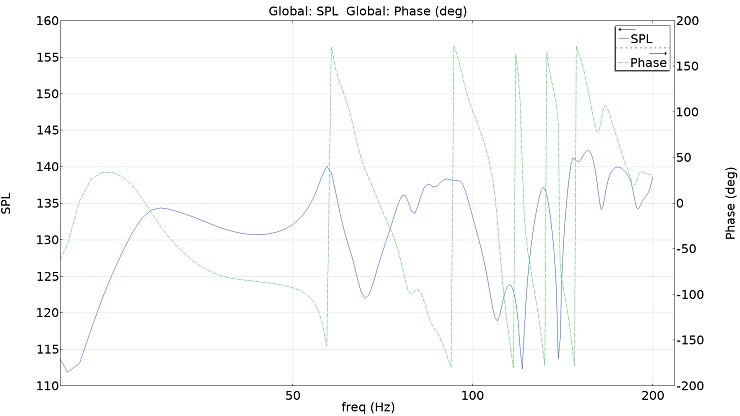
Abb. 9: Amplituden- und Phasenfrequenzgang eines kleinen Studios mit ersten simulierten Bassabsorbern
Ressourcen-Hunger
FEM-Simulationen sind, wie bereits erwähnt, ihrer Natur nach sehr Rechenintensiv und benötigen viel Arbeitsspeicher. Je nach Komplexität und Granularität des Polygon-Gitters und der oberen Grenzfrequenz der Analyse, dauert die Berechnung einer Variante auf einem Standardrechner schnell einmal mehrere Stunden oder auch Tage. Aufgrund der Rechnerleistungen wäre es aber noch vor wenigen Jahren gänzlich undenkbar gewesen, derartige Simulation ausserhalb einer (universitären) Grossrechner-Umgebung überhaupt auszuführen.
Um die Berechnungen zu beschleunigen, lautet die Empfehlung also: "Kauf Dir einen schnelleren Computer". Am effektivsten setzt man allerdings spezialisierte, lokale oder cloudbasierte Server-Strukturen ein, die den Zugriff auf mehrere Hundert Hochleistungs-Prozessor-Kerne und mehrere Terabyte RAM-Speicher ermöglichen.
Der Akustiker, der das Glück hat, auf solche Ressourcen zugreifen zu können, kann dann immer noch entscheiden, ob er sich das Feierabendbier etwas früher am Tage gönnt (was dann allerdings regelmässig bereits am früheren Vormittag der Fall sein dürfte und deshalb auf Dauer womöglich der Gesundheit nicht sonderlich zuträglich ist); oder ob er in der gleichen Zeit sehr viel mehr Varianten durchspielen will, um das bestmögliche Ergebnis zu evaluieren. Um sowohl die Qualität des Endergebnisses als auch das persönliche Wohlbefinden und Glücksgefühl gebührend zu berücksichtigen, empfiehlt sich - wie so oft im Leben - ein sinnvoller Mittelweg. Zum Wohl!
Abb. 10: Ein Akustiker lässt sich zum Bier verführen (Foto und Bearbeitung: B. Rufer)
Fragen, Kommentare, Newsletter-Anmeldung
Hat Ihnen dieser Artikel gefallen? Möchten Sie mehr davon? Haben Sie Anmerkungen oder Fragen? Schreiben Sie mir eine E-Mail: info@zehner.ch oder füllen Sie untenstehendes Formular aus. Gerne informiere ich Sie mit meinem Newsletter auch über Überarbeitungen und neue Artikel auf diesen Seiten.
Warten Sie nach dem Absenden des Formulars, bis die Bestätigungsseite erscheint!